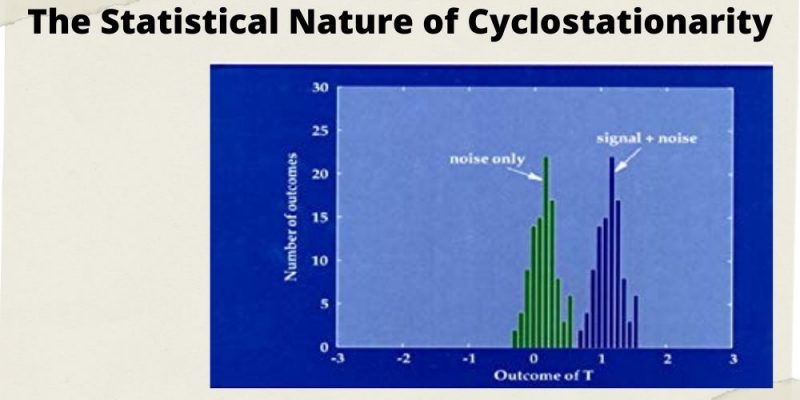
The cyclostationarity method consists of statistical properties which differ cyclically over time. A cyclostationary process can be regarded as several interleaved static functions.
For example, the maximum regular temperature of New York City can be modeled as a cyclostationary process: the highest temperature on July 21 is statistically differs from its temperature on December 20; though, it is a reasonable assumption that the temperature on December 20 of various years has similar statistics.
Hence, we can view the random method composed of daily highest temperatures as 365days interleaved in stationary processes; each takes a new value per year. An essential particular case of cyclostationary signals exhibits cyclostationarity statistically in second-order (e.g., the autocorrelation function).
These are known as wide-sense cyclostationary signals, which are analogous to wide-sense stationary processes. The Perfect definition varies based on whether the signal is dealt with as a stochastic processor in a deterministic time series.
Different Approaches Of Cyclostationarity
There is two way of approaches to the utilization of cyclostationary processes. The probabilistic technique is to notice measurements as an event of a sochastic process. However, being an alternative, the deterministic way is to track the measurements with single time series.
A probable distribution for a few events connected with the time series can be elaborated as the fraction of time, which occurs throughout the lifelong of the time series. In both the treatment, the time series is cyclostationary, only if its associated probability distributions vary periodically over time.
However, in the deterministic time-series approach, we have an alternative but equivalent clarity: A time series which contains no finite-strength and additive components of sine-wave is found to ground cyclostationarity, only if there is the existence of some time-invariant transformation, non-linear, of the time series which can generate positive-strength of additive sine-wave components.
Possibly, one can generalize the sections of autoregressive moving average models to associate cyclostationary functions. For instance, Troutman treated autoregressions where the autoregression coefficients and the residual variance are not constant but differ cyclically over time. His work follows a count of other research of cyclostationary methods within the area of time series analysis.
Uses Of Cyclostationarity Process
- Cyclostationarity is followed in Telecommunications to deploy signal synchronization;
- In Econometrics, cyclostationarity enables analysis of the periodic behavior in financial markets;
- Queueing theory depends on cyclostationary idea to experiment with car traffic and computer networks
- Cyclostationarity allows tracking mechanical signals generated by reciprocating and rotating machines.
Angle-time cyclostationarity: Mechanical Signal
Mechanical signals generated from the rotation and reciprocation of machines are notably well modeled as cyclostationary methods. The cyclostationary family allows all signals with the hidden periodicities, either of the additive kind (existence of tonal components) or multiplicative (presence of periodic modulations).
It happens to be the instance for vibration and noise produced by the gear bearings, gear mechanisms, turbofans, internal combustion engines, propellers, pumps, etc. The unique modeling of mechanical signals as cyclostationary processes has been found beneficial in several applications, such as NVH- Noise, Vibration &Harshness; in condition to monitor.
In the latter ground, cyclostationarity is found to generalize the technique of envelope spectrum, a popular analysis method utilized in the diagonalization of bearing faults.
The peculiarity in rotating machine signals is the span of the method is strictly connected to the rotational angle of the specific component – the “cycle” of the machinery. While, at the same time, a brief description needs to be preserved to reflect the nature of dynamic phenomena governed by several equations of time. Hence, the function of angle-time autocorrelation is used.
Wrap Up – Future Trend Of Cyclostationarity
There are few limits to the applications of the cyclostationary model that the restoration of generalizing cyclostationarity can overcome. The generalizations consist of one of the future ways in the field.
Limits to the deployment of the cyclostationary model arising from probable imperfections in the pace of the everyday phenomena underlying the recorded signal, defects which become evident on more significant observation intervals.
These irregularities can be caused, for instance, by little time variability of time parameters or by the related motion within transmitter and receiver. Two extended ways of the cyclostationary model have been proposed for more excellent fidelity form of communications signals in higher mobility scenarios.
A further classification has been submitted to define evidence where statistical cyclicity is irregular in the data, such as biological signals. Specific, cyclostationary signals have been referred to be a perfect model for processes that exhibit irregular cyclicity. This section of signals includes clear amplitude-modulated and time-warped almost-cyclostationary signals.
Read More : What is Cyclostationarity Feature Detection?